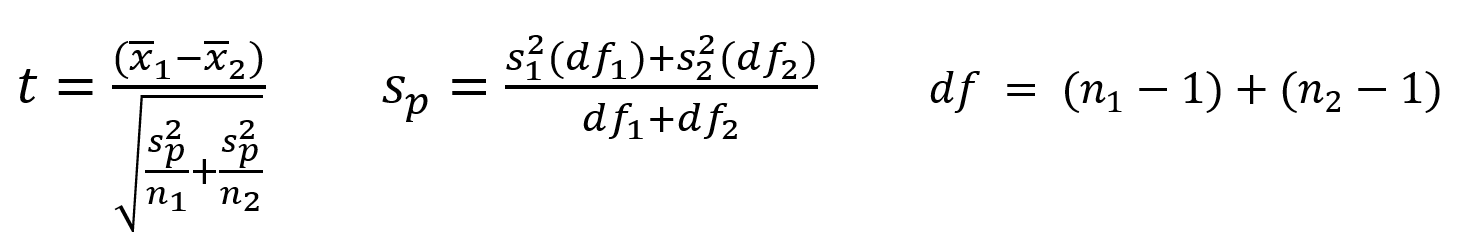
djhasem.blogg.se - Two dependent means hypothesis test calculator

#Two dependent means hypothesis test calculator how to

To compare two means or two proportions, one works with two groups. The general procedure is still the same, just expanded. You will compare two means or two proportions to each other. We will expand upon that in this section.

#Two dependent means hypothesis test calculator how to

In the previous section, we explained how to conduct hypothesis tests on single means and single proportions. Students are interested in whether SAT or GRE preparatory courses really help raise their scores. Politicians compare the proportion of individuals from different income brackets who might vote for them. For example, studies compare various diet and exercise programs. There are other situations that deal with the comparison of two groups.

Then, the heart attack rate is studied over several years. Typically, one group is given aspirin and the other group is given a placebo. Over the last few years, newspapers and magazines have reported about various aspirin studies involving two groups. For example, researchers are interested in the effect aspirin has in preventing heart attacks.

independent group: A statistical group of random variables that has the same probability distribution as the others, and that are all mutually independent.

matched pair: A data set of two groups consisting of two samples that are dependent.

Matched pairs consist of two samples that are dependent.

Independent groups mean that the two samples taken are independent, that is, sample values selected from one population are not related in any way to sample values selected from the other population.

The groups are classified either as independent or matched pairs.

The following examples show how you can conduct this type of test using summarized data.ĩ.2.2.1.1 - Example: Summarized Data 9.2.2.1. We are 95% confident that the mean difference in the population is between -5.16 and 45.78. Note that we could also interpret the confidence interval in this output. There is not evidence to state that the mean SAT-Math scores of students who have and have not ever cheated are different. Our p-value is greater than the standard alpha level of 0.05 so we fail to reject the null hypothesis.

The result of our two independent means t test is \(t(95) = 1.58, p = 0.117\). \(\mu_2\): mean of SATM when Ever_Cheat = YesĮqual variances are not assumed for this analysis. \(\mu_1\): mean of SATM when Ever_Cheat = No We are 95% confident that the mean difference in traditional students' and adult learners' final exam scores is between -0.689 points and +2.069 points.ĩ.2.1.1 - Minitab: Confidence Interval Between 2 Independent Means 9.2.1.1 - Minitab: Confidence Interval Between 2 Independent Means \(point \ estimate \pm (multiplier) (standard \ error)\) Now, we can combine all of these values to construct our confidence interval: To find the multiplier, we need to construct a t distribution with \(df=smaller\ n-1=138-1=137\) to find the t scores that separate the middle 95% of the distribution from the outer 5% of the distribution: The standard error can be computed next: \(\sqrt=0.697\)

The point estimate, or "best estimate," is the difference in sample means: \(\overline x _1 - \overline x_2 = 41.48-40.79=0.69\) She wants to construct a 95% confidence interval to estimate the mean difference. She collected the following data from a sample of students: Descriptive Statistics A STAT 200 instructor wants to know how traditional students and adult learners differ in terms of their final exam scores.